Contents
A combination of increasing demand for new drugs and advances in automation have made high-throughput screening of chemical compounds a reality. Image-based screens, in particular, can measure hundreds of cellular features at the single-cell level and are therefore of great interest.
In this small rotation project, I optimized the usage of existing computational tools for the analysis of image-based chemical screens at the single-cell level.
##Background While there is increasing need for the discovery of new drugs, the number of new approved drugs per decade is in fast decline. In response to this, high-throughput screening of chemical compounds is a tool that is increasingly more used and in high demand due to its ability to investigate hundreds of thousands of compounds in a relatively short time.
Image-based screens are able to measure hundreds of cellular and sub-cellular features quantitatively and are therefore extremely powerful. Although generally slower than other screening methods, the amount and variety of data acquired in high-throughput image-based screening is unsurpassed. It’s ability to have single-cell measurements is a quality which only very recently is starting to be acquired in other fields of molecular biology, and thus makes it by excellence a data-rich method.
Of particular interest is the ability of these screens to probe into the cell-to-cell variability of responses to perturbations, where the population context of cells can be a determinant condition to respond in variable ways when perturbed.
I know citations are due here, I'm looking into https://github.com/inukshuk/jekyll-scholar to do that in the best way.
##Results To obtain objects from the images captured in the screen, object detection using Cell Profiler was performed. This was performed by manually adjusting detection parameters (see Methods section). Based on previously identified objects from the raw signal (Figure 1A-D), other cellular features can be inferred (Figure 1E) and several metrics dependent on the detected objects can be computed (Figure 1F).
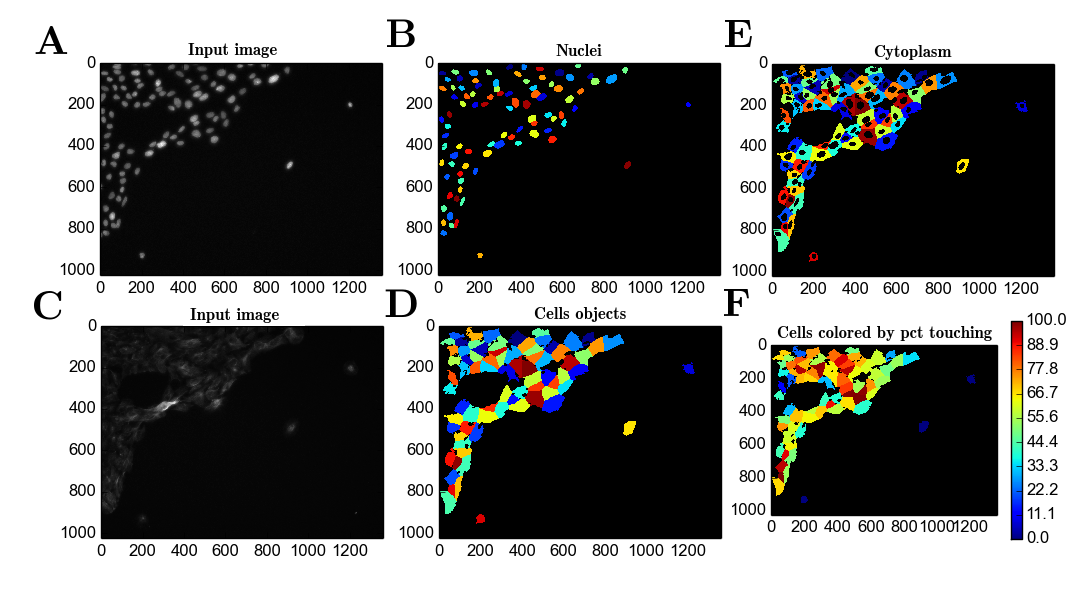
Figure 1 - A) Raw signal from the DAPI channel; B) Nuclei object detection; C) Raw signal from the Alexa488 channel; D) Detection of objects representing $\beta$-tubulin staining; E) Inferred cytoplasm objects based on the detection of B) and D); F) Color-coder cell objects based on the percentage of surface in contact with other cell objects (neighbours).
Objects representing cells were detected and their properties were quantified in over 200 variables. To reduce complexity mean measurements per well were first used to describe inter-well variability.
Due to position-dependent differences in the conditions for cell growth, plate-dependent effects are noticeable on virtually every cellular measurement taken during the screen. To neutralize this, measurements were normalized by taking into account the cell’s position on the plate (see methods). Normalization of the bias is noticeable (Figure 2) and in the case of measurements capable to distinguish cell viability (e.g. number of cells, cell area), led to generally higher Z-factor scores for that measurement. Normalization not only corrects experimental biases but improves the ability to compare wells with different treatments and therefore distinguish between negative and positive controls - e.g. notice the difference between wells in diagonals (positive controls) in raw versus normalized data in Figure 2B.
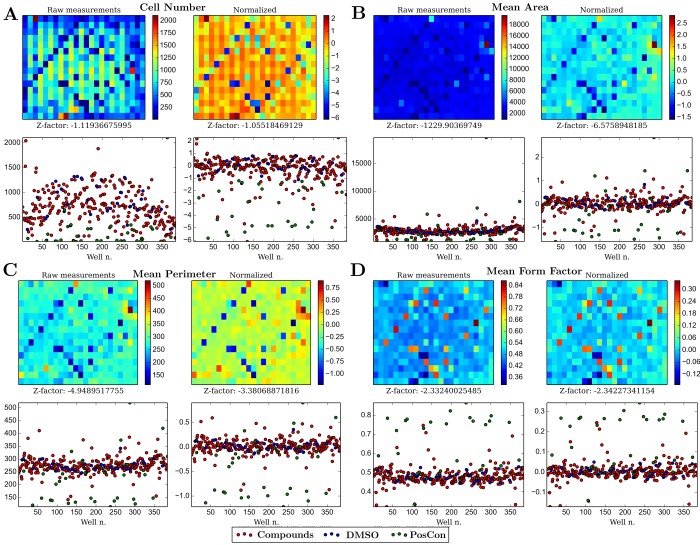
Figure 2 - Comparison between raw and normalized data of four cellular measurements: A) Cell numbers per well; B) Average area per well C) Averaged perimeter per well D) Averaged cellular form factor per well. For each measurement, the left panels use raw data, whereas the right ones use data normalized as described in the methods section. The upper panels represent data preserving the positional information of the 384-well plate used in the screen.
Since no single measurement is able to perfectly discriminate the cellular response to the chemical treatment, relationships between different measurements were observed.
In accordance with expectations, some measurements revealed a high degree of correlation due to their intrinsic physical relationships. Mean cellular area and perimeter are naturally correlated (Figure 2A) and this is not particularly informative since these cellular properties are maintained during cellular growth or death. Cell number and measurements of cellular form factor are anti-correlated (Figure 2B), showing that the second measurement is detecting changes in cellular shape as the number of cells in a well diminishes. Measurements of overall cellular shape, seem therefore better fitted than measurements of cellular dimension to discriminate between positive and negative controls either when in combination (Figure 2C) or when compared with other cellular measurements (Figure 2D).
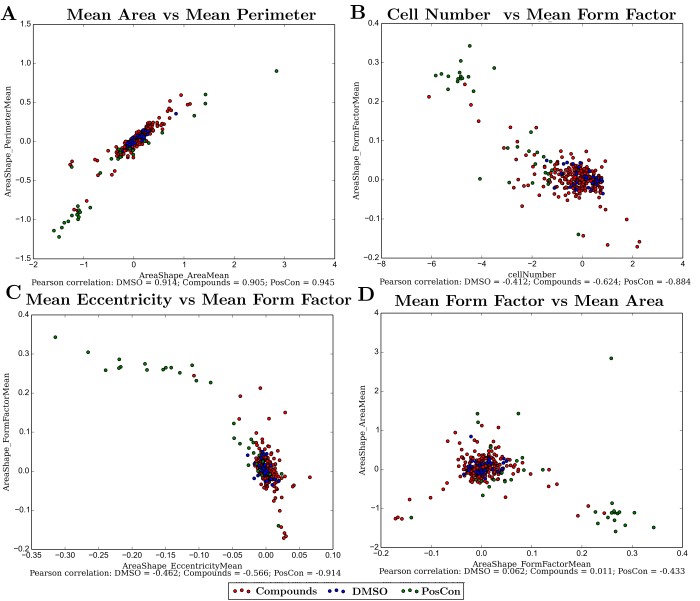
Figure 2 - Relationship between some of the cellular measurements. A) Area and perimeter; B) Cell number and cellular form factor; C) Eccentricity and form factor; D) Form factor and area. All measurements (except cell number) are averages from each well. Pearson correlation coefficients are shown for values within groups of wells under the same category (Negative control: DMSO; Positive controls: PosCon; and treatments with several compounds: Compound).
To explore the variability of cellular response to the same chemical perturbation under the same conditions, I took advantage of the power of this screen to measure single-cells. Variability can be observed as a density function produced for each well (Figure 4). The general shape of the distribution in most measurements resembles a Gaussian distribution, showing that the majority of cells exposed to the same stimuli respond equally. Nevertheless, for some compounds it is possible to notice variable response within the cellular population exposed to it, forming sub-populations. The existence of sub-populations can be explained by technical artefacts such as cell death and fragmentation during the immunostaining procedure, incorrect detection of cellular objects, but the existence of a true differential response to a compound from cells can also be due to differential population contexts.
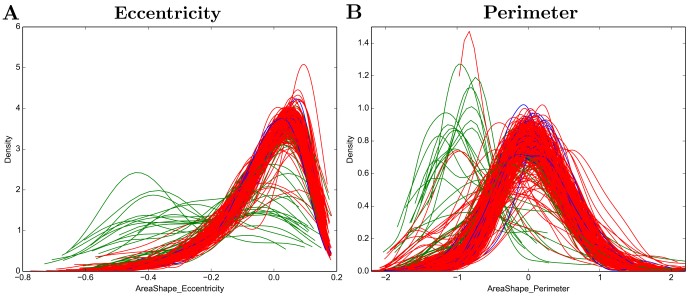
Figure 3 - Density plots of A) Cell shape eccentricity and B) Cell perimeter per well.
Due to the high-information content nature of the screen, a very interesting approach to detect compounds with a relevant effect in overall cellular biology would be to use machine learning to distinguish between normal cellular states and states revealing an effect of the compound. I trained a Support Vector Machine (SVM) using a linear model in a classification task to distinguish between cells treated with DMSO or with a compound used as a positive control.
As a first step, I used both subsets (12 to 48 measurements) and the whole group (independently) of both cellular or nuclear measurements of shape and intensity in a Principal Component Analysis (PCA) approach to provide the SVM with a two-dimensional input (Figure 4). Models were used to classify all cells that were in wells treated with chemical compounds but unexpectedly none of the attempted training events using any of the combinations of staring cellular or nuclear measurements yielded a model capable of classifying any of the cells in wells treated with compounds as affected by the compound as the cells in the positive control wells. Nevertheless, it is possible to observe that such cells must exist, as can be observed by the shift in the density towards the location where most cells in positive control wells are located as measured by some variables independently such as demonstrated in Figure 4.
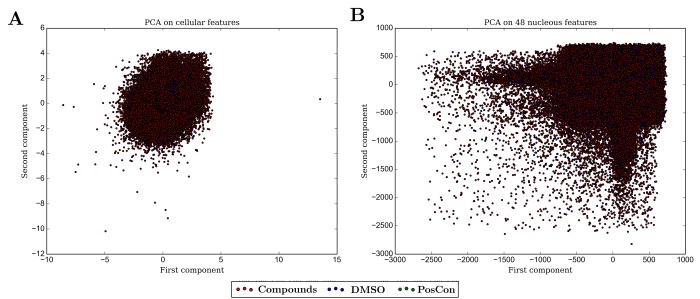
Figure 4 - Principal component analysis of A) 12 cellular measurements; B) 48 measurements of nuclei features.
##Discussion While many measurements of cell dimensions, shape, intensity of signal are correlated with the cellular responses to the chemical treatment, it is clear no single measure is fit to evaluate it to a sufficient degree - therefore, methods that integrate several measurements are of great interest.
All of our attempts to use a SVM classifier to detect compounds with effects similar to the ones used as positive controls failed. The main drawback probably lies in the requirement of SVM models to be fed with low dimension data. The use of a PCA approach to reduce dimensionality is counterproductive since it promotes severe loss of information and does not necessarily guarantee dispersion of classes as shown in Figure 4. Many of the variables might not be informative at all, increasing noise levels into the data and clouding the training step of machine learning. It is also possible that the distribution of cellular responses to treatments with a vast array of compounds is not linear and therefore a linear classifier would also not be appropriate.
##Methods Cell Profiler was used to automate image analysis on the images obtained from four fields in each well of the 384-well plate. This software allows detection of objects based on the signal of the three channels used in this assay - DAPI for nuclei, Alexa488 for $\beta$-tubulin and MitoTrackerOrange staining for mitochondria.
An approach to identify cellular features based on the fluorescent signal from the images was designed, allowing the establishment of relationships between them and can build on other classes of objects already identified. Two primary objects (nuclei and mitochondria) were identified based on the source of fluorescent signal from the DAPI and MitoTrackerOrange stainings, respectively. Secondary objects representing whole cells were collected by propagation from the nuclei objects until the border of signal from the Alexa 488 channel using a global thresholding strategy with the Otsu algorithm. While identifying both primary and secondary objects, objects that touched the image border were discarded. If this occurred to the secondary object, the primary object used for the propagation was discarded as well to avoid the existence of unpaired primary-secondary objects. Cytoplasm was identified as a Tertiary object through the subtraction of the nuclei area from the area of the cell objects, therefore establishing a relation between a cell’s nuclei and cytoplasm. Relationships between cell and mitochondria objects were established by intersecting the location of mitochondria with the cells and each overlapping mitochondria object was annotated with its respective parent cell.
For each object identified, measurements of signal intensity of all channels, area and shape were taken. Measurements of euclidean distances between all objects within and between classes were taken, including pairs of parent-child objects.
Since Cell Profiler’s capabilities lied mainly in object discovery and measurement, data was exported to a HDF5 file and analysis proceeded in a custom-built script heavily based on Python and the Pandas library, therefore allowing great flexibility and control over operations. Normalization of measurements was performed to compensate biases in cellular growth conditions due to the cell’s position in the plate wells. This was performed for each cell by subtracting the median of all cell measurements in its row and column. For measurements which naturally possess high global variance, values were transformed with a logarithm of base 2.
For all measurements, a measure of its ability to distinguish between negative and positive controls (Z-factor) was calculated as described by Zhang \cite{Zhang1999} and shown in equation 1:
\[Z = 1 - \left( 3 \times \left(\frac{SD \left(Pos \right ) + SD \left(Neg \right )}{abs \left(mean \left (Pos \right ) - mean \left (Neg \right )\right )}\right )\right )\]In the analysis of single-cell variation, I chose 12, 20, 31 and 48 different measurements of nuclei shape, intensity and area, performed Principal Component Analysis (PCA) on those variables to reduce dimensionality to two variables. A Support Vector Machine (SVM) linear classifier was trained on the two-variable data from cells in negative and positive control wells of two plates and ran the classifier model on all cells treated with the chemical compounds.
High-throughput image-based chemical screens yield a high amount of data in the form of images. The analysis of this kind of data can be particular challenging due to their subjective nature. With the development of feature-detection from images and machine learning algorithms, the task of detecting, quantifying and classifying objects is becoming increasingly easy. Nonetheless, detection of cellular features in images still requires optimization due to the variability between cellular phenotypes which arise naturally between different cell lines, but are exacerbated when these are perturbed.
##Code This is basically just a dump of code I used, I need to revisit it.